La trigonometría desempeña un papel vital en la determinación de las distancias entre los cuerpos celestes. Al medir el ángulo de paralaje, los astrónomos pueden calcular la distancia a las estrellas cercanas. El paralaje es el desplazamiento aparente en la posición de un objeto cuando se observa desde diferentes puntos de vista. Los astrónomos miden el ángulo de paralaje desde la Tierra en dos momentos diferentes, separados por seis meses, cuando la Tierra se encuentra en lados opuestos de su órbita. Aprovechando los principios trigonométricos simples, pueden calcular la distancia a la estrella utilizando relaciones trigonométricas.
2. Navegación celestial
La trigonometría también ayuda a navegar por la vastedad del cielo nocturno. En el pasado, antes de que la tecnología de navegación estuviera avanzada, los marineros se basaban en las estrellas para navegar durante sus viajes. Utilizaban cuerpos celestes, como la Estrella del Norte (Polaris), para determinar su latitud. Al medir el ángulo entre el horizonte y la estrella, los marineros podían calcular su distancia al ecuador. Este proceso implicaba el uso de ecuaciones trigonométricas que relacionan ángulos y distancias.
3. Determinación de tamaños y masas
La trigonometría ayuda a los astrónomos a determinar los tamaños y masas de los objetos celestiales. Al analizar los tamaños aparentes de los objetos en relación con sus distancias, los astrónomos pueden estimar sus tamaños reales. Este método es particularmente útil cuando se estudian objetos que están demasiado lejos para medir directamente, como galaxias y cuásares. Además, los principios trigonométricos se pueden aplicar para medir las masas de los sistemas binarios de estrellas, donde dos estrellas orbitan alrededor de un centro de masa común.
4. Comprensión de los triángulos cósmicos
El estudio de los triángulos está en el corazón de la trigonometría y encuentra una amplia aplicación en la astronomía. Los astrónomos a menudo trabajan con triángulos cósmicos formados al conectar tres cuerpos celestes. Observando los ángulos y lados de estos triángulos, los astrónomos pueden recopilar información esencial sobre las distancias y posiciones de los objetos involucrados. Este conocimiento les permite construir modelos precisos de sistemas celestiales y estudiar su dinámica.
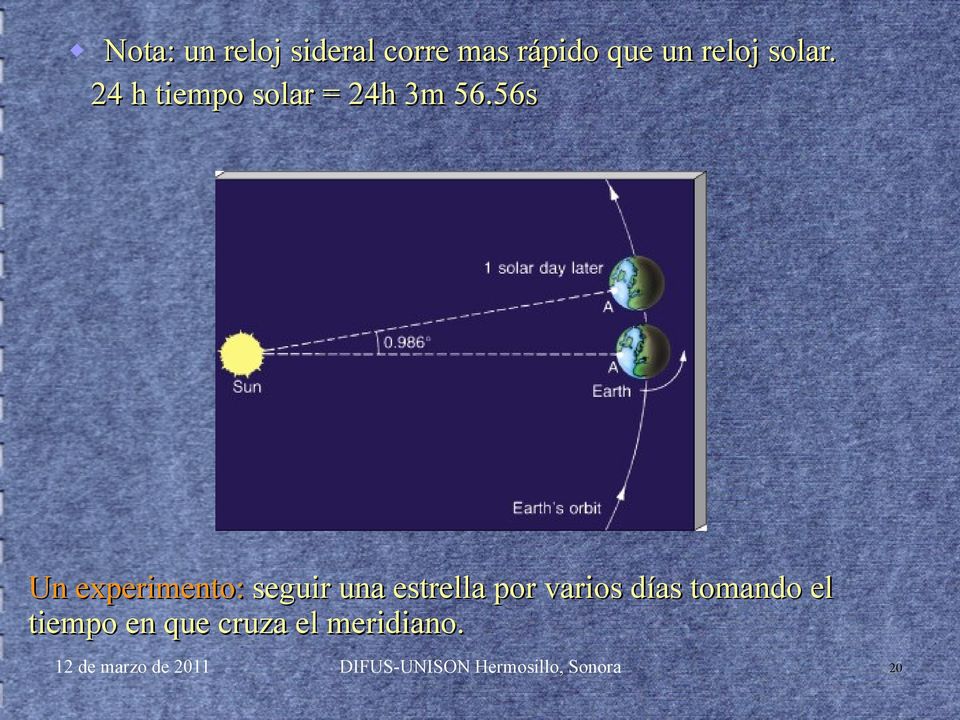
5. Rastreo del movimiento estelar
La trigonometría proporciona a los astrónomos los medios para rastrear el movimiento de las estrellas y otros objetos celestiales a lo largo del cielo nocturno. Al medir la posición de un objeto en diferentes momentos, pueden determinar su velocidad y trayectoria. Los cálculos trigonométricos permiten a los astrónomos medir con precisión el movimiento propio de las estrellas, que se refiere a su movimiento aparente a través del cielo con el tiempo. Esta información es crucial para comprender la dinámica y la evolución de los cúmulos estelares y las galaxias.
Conclusión
La astronomía depende en gran medida de la trigonometría para numerosos cálculos y mediciones. Al utilizar los principios de la trigonometría, los astrónomos pueden determinar distancias, navegar a través del espacio, estimar tamaños y masas, interpretar triángulos cósmicos y rastrear con precisión el movimiento de los objetos celestiales. La sinergia entre la trigonometría y la astronomía ha contribuido significativamente a nuestra comprensión del universo y continúa desentrañando sus secretos. Entonces, la próxima vez que contemples el cielo nocturno, recuerda que la belleza del cosmos está entrelazada con la belleza de la trigonometría.